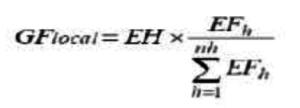Conforme comentei recentemente, o valor da energia firme (média de geração entre junho de 1949 e novembro de 1956, obtida por simulação) é decisivo na obtenção da garantia física[1] de uma UHE (usina hidrelétrica com potência instalada maior que 30 MW). A perda de carga hidráulica, por sua vez, é fundamental no cálculo da energia firme: quanto maior este valor, menor a geração. O artigo apresenta a análise de um aspecto operacional da perda hidráulica considerada nos modelos de simulação energética.
Sob condições especiais que facilitam a análise (uma usina com circuito curto, por exemplo), a perda de carga hidráulica (Perdah, em metros) do circuito de geração de uma UHE pode ser dada por:
Perdah = K x Q² (1)
Onde K é um coeficiente, em s2/m5, que depende do circuito em questão e Q é a vazão passando por cada uma das turbinas: esta vazão é limitada fisicamente por um valor QMAXA, a vazão máxima de engolimento da turbina. Como a vazão afluente às turbinas de uma UHE é variável no tempo, conclui-se, pela a fórmula (1), que a perda de carga também o é. O modelo Suishi, do Cepel, que é o programa oficial para o cálculo da energia firme[2], não permite que a perda hidráulica seja utilizada considerando a fórmula (1). O programa possibilita dois tipos de entrada para este parâmetro:
a. Perda constante em metros.
b. Perda como um percentual da queda bruta.
Como o critério (a) é o usual em cálculo de garantia física[3], é este o que será analisado no presente artigo.
A partir disso, o problema que se coloca é o seguinte: como compatibilizar um parâmetro variável ao longo do tempo, conforme a fórmula (1), com outro que é constante, para entrada no modelo Suishi? Um critério que parece, intuitivamente, ser o mais correto para resolver esta questão seria fazer pares de simulações iterativas:
i. Simulação com o Suishi levando em conta uma perda de carga constante arbitrada.
ii. Simulação de reprodução da operação do Suishi em planilha, mas considerando a fórmula (1). Os estudos de Viabilidade para o Leilão da UHE Sinop, por exemplo, mostram um exemplo deste tipo de simulação energética em planilha[4].
A perda constante escolhida seria aquela que igualaria as energias firmes obtidas em (i) e (ii), após uma série de iterações.
A simulação (ii) envolve dois aspectos importantes, ambos relacionados à vazão máxima de engolimento QMAXA, conforme segue.
A queda líquida de uma UHE é dada pela diferença entre os níveis de montante e de jusante, subtraída ainda das perdas hidráulicas: estas três variáveis são variáveis no tempo, de modo que a queda líquida também o é. Na grande maioria dos casos, a vazão máxima de engolimento QMAXA é máxima na chamada queda de referência (href) e menor nos outros casos:
A. quando a queda líquida é menor que href, QMAXA diminui devido a limitações de turbina;
B. quando a queda líquida é maior que href, QMAXA diminui devido a limitações do gerador[5].
A partir do exposto, conclui-se que é necessário um cálculo iterativo quando a vazão afluente às turbinas é relativamente alta, já que a a perda hidráulica depende de QMAXA, conforme a fórmula (1), e QMAXA depende da queda líquida (conforme itens A e B, acima), parâmetro que, por sua vez, depende da perda hidráulica[6].
O cálculo iterativo apresentado anteriormente pode ser resolvido sem grande dificuldade.
Por outro lado, conforme se apresentará a seguir, o outro aspecto a ser analisado sobre a consideração das perdas de carga no Suishi quando a vazão afluente é próxima a QMAXA não tem uma solução viável.
Conforme o Manual de Referência do Modelo Suishi[7], a vazão máxima de engolimento efetivamente considerada pelo modelo, QMAX, é igual a QMAXA multiplicada por FCMAXL, o fator de capacidade máximo, dado pelo complemento da indisponibilidade total (forçada + programada)[8]. Supondo, por exemplo, que a indisponibilidade total seja igual a 10%, FCMAXL é dado por seu complemento, ou seja: (1 – 10/100) = 0,9.
Isto faz com que na prática, em circunstâncias normais (indisponibilidade maior que zero), a vazão máxima de engolimento considerada pelo Suishi é menor que o seu valor real. Um exemplo simples ajuda a explicar o problema: seja uma UHE com apenas uma turbina, com vazão máxima real (QMAXA) igual a 100 m³/s, K igual a 0,00001 s2/m5, e uma indisponibilidade total igual a 10%. Neste caso, a vazão máxima de engolimento efetivamente considerada pelo modelo (QMAX) será igual a 90 m³/s. Em termos de perda de carga, a perda máxima real (fórmula 1) é igual a 0,00001 x 100² = 0,10 m, enquanto que a realmente enxergada pelo modelo é igual a 0,00001 x 90² = 0,08 m.
O exposto mostra a dificuldade em se fazer com que o modelo Suishi reproduza uma equação real de perda de carga na simulação energética. Este tipo de erro pode ser considerado de segunda ordem mas, dados os valores financeiros expressivos envolvidos no cálculo e utilização da garantia física de UHEs, poder-se-ia pensar em alguma modificação na simulação do modelo para aproximar a operação real com a computacional neste caso.
Artigo posterior irá aprofundar um pouco mais esta questão.
***
Algumas das questões envolvidas no texto acima são aprofundadas nos seguintes artigos científicos, que escrevi juntamente com Roberto Eugenio Bertol:
- Muller, F.; Bertol, R. E. Analysis of the influence of hydrology and the number of units influence in the average hydraulic loss. Revista Espaço Energia. Curitiba, Brasil, abril de 2014.
- Muller, F.; Bertol, R. E. Comparison between fixed and variable head losses in energy simulation. Revista Espaço Energia. Curitiba, Brasil, outubro de 2016.
- Muller, F.; Bertol, R. E. Análise de perdas de carga no MSUI. Revista Brasileira de Engenharia de Barragens, ano I, n. 1, p. 8-13, 2014.
- Muller, F.; Bertol, R. E. Análise da indisponibilidade no MSUI 1. Relação entre vazão máxima turbinada e vazão média afluente. In: XX Simpósio Brasileiro de Recursos Hídricos, 2013, Bento Gonçalves. Porto Alegre: Associação Brasileira de Recursos Hídricos, 2013.
- Muller, F.; Bertol, R. E. Análise da indisponibilidade no MSUI 2. Permanência de vazões afluentes. In: XX Simpósio Brasileiro de Recursos Hídricos, 2013, Bento Gonçalves. Porto Alegre: Associação Brasileira de Recursos Hídricos, 2013.
_______________________________
[1] quantidade limite de energia que os geradores podem vender em contratos
[2] conforme a Portaria MME Nº 101 DE 22/03/2016
[3] ver, por exemplo, o relatório “Revisão Ordinária de Garantia Física de Energia das Usinas Hidrelétricas Despachadas Centralizadamente no Sistema Interligado Nacional – SIN”, do MME. Link: < http://www.mme.gov.br/documents/1138787/13719261/Relat%C3%B3rio+Final_25Abril2017.pdf/37ce6a5b-3e18-4322-995e-52d77c60a5c6 >
[4] relatório “Modelagem Energética da UHE Sinop”, da EPE – Empresa de Pesquisa Energética (2010)
[5] ver maiores detalhes na página 53 do Manual de Referência do Modelo Suishi, versão de abril de 2018
[6] além disso, a queda líquida também depende do nível de jusante, que por sua vez, depende das vazões afluente e turbinada
[7] do Cepel, na versão de abril de 2018
[8] em termos algébricos, FCMAX = (1 – TEIF/100) x (1 – IP/100), onde IP é o coeficiente de indisponibilidade programada e TEIF o coeficiente de indisponibilidade forçada, ambos em %